
The further apart these are, the more accurate your reading will be. You will need to take two angular measurements of the height of the kite above the horizon. The angle that you want to measure is the one marked in yellow in the diagram.

The plumb line must be able to swing freely from the centre of the protractor. It will help if the protractor has a small tube attached to it to help sighting the kite accurately when you measure its angle above the horizon. a tape measure (or you can pace out the distance).To calculate the height of your kite you will need: My method uses the same principle, but without the drawing. Most people (including me) just estimate the length of the line and make a guess at the height based on that and the angle the kite is flying at.ĭavid Pelham’s book Kites gives a method that ignores the length of the line, but involves drawing accurate scale diagrams - not so easy to do in the field. It’s a question that’s not that easy to answer accurately. There are numerous other proofs ranging from algebraic and geometric proofs to proofs using differentials, but the above are two of the simplest versions.One of the most common questions I am asked when flying single line kites is, “How high is it?” I guess it’s the same for most kite flyers. Which is again, the Pythagorean equation. Since the larger square has sides c and area c 2, the above can be rewritten as: The area of the larger square must then equal the sum of the areas of the four triangles and the smaller square such that: (b - a) 2 + 4 The four triangles with area abĪlso form a larger square with sides of length c. In the second orientation shown in the figure, ii, the four copies of the same triangle are arranged such that they form an enclosed square with sides of length b - a, and area (b - a) 2. The sum of the area of these four triangles and the smaller square must equal the area of the larger square such that: (b + a) 2 = c 2 + 4
This results in the formation of a larger square with sides of length b + a, and area of (b + a) 2. In the first one, i, the four copies of the same triangle are arranged around a square with sides c. In the figure above, there are two orientations of copies of right triangles used to form a smaller and larger square, labeled i and ii, that depict two algebraic proofs of the Pythagorean theorem. There are a multitude of proofs for the Pythagorean theorem, possibly even the greatest number of any mathematical theorem. If the angle between the other sides is a right angle, the law of cosines reduces to the Pythagorean equation.
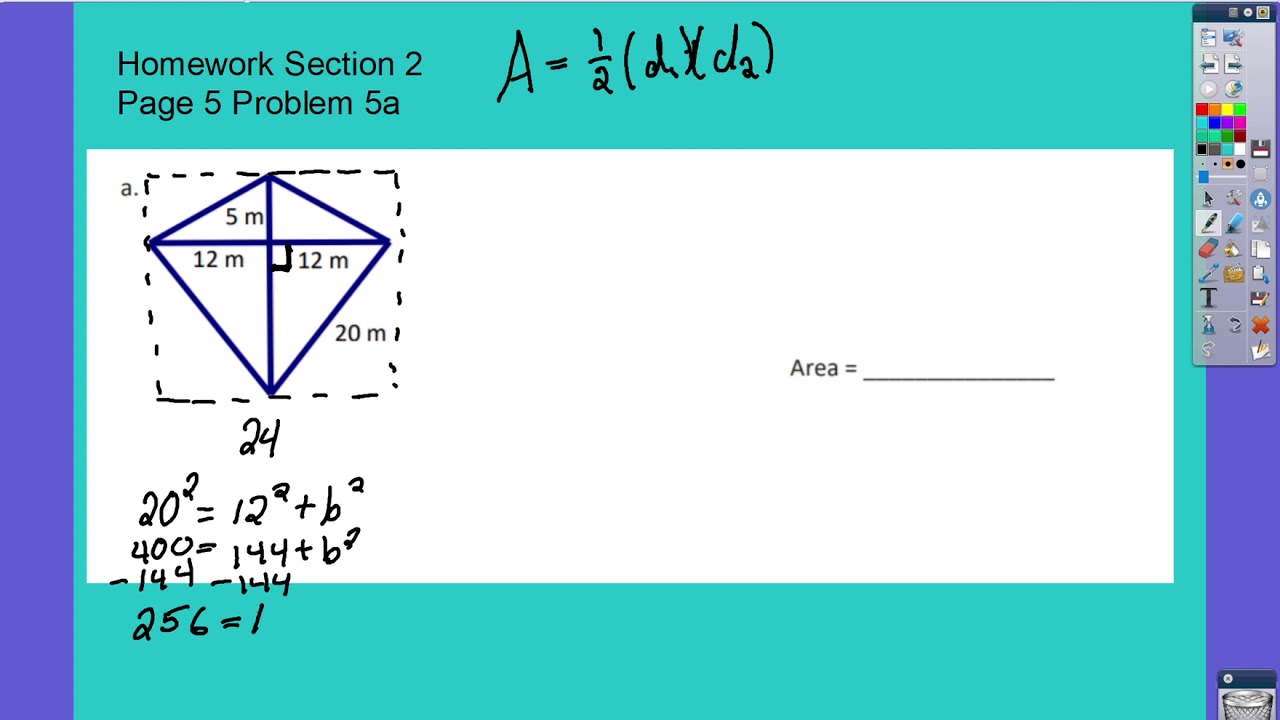
The law of cosines is a generalization of the Pythagorean theorem that can be used to determine the length of any side of a triangle if the lengths and angles of the other two sides of the triangle are known. It follows that the length of a and b can also be determined if the lengths of the other two sides are known using the following relationships: This relationship is useful because if two sides of a right triangle are known, the Pythagorean theorem can be used to determine the length of the third side. This is known as the Pythagorean equation, named after the ancient Greek thinker Pythagoras. In other words, given that the longest side c = the hypotenuse, and a and b = the other sides of the triangle: Given a right triangle, which is a triangle in which one of the angles is 90°, the Pythagorean theorem states that the area of the square formed by the longest side of the right triangle (the hypotenuse) is equal to the sum of the area of the squares formed by the other two sides of the right triangle: The Pythagorean Theorem, also known as Pythagoras' theorem, is a fundamental relation between the three sides of a right triangle. Related Triangle Calculator | Right Triangle Calculator


 0 kommentar(er)
0 kommentar(er)
